E-DQAS for the Transverse Field Ising Model - A Framework for Symmetry-Informed Algorithm Discovery

Abstract

The design of quantum circuits for near-term hardware presents a significant challenge, requiring a delicate balance between physical accuracy and practical executability. For many important physical systems, respecting fundamental symmetries is not merely a preference but a requirement for a valid solution. We introduce an advanced application of our Enhanced Differentiable Quantum Architecture Search (E-DQAS) platform, now re-engineered to treat physical symmetry as a non-negotiable guiding principle. This work moves beyond simple energy minimization to a sophisticated, physics-informed discovery process.

View Related Publications

GitHub Repo : https://github.com/Apoth3osis-ai/e-dqas_qiskit_transverse-field

Research Gate: https://www.researchgate.net/publication/392760288_E-DQAS_for_the_Transverse_Field_Ising_Model_A_Framework_for_Symmetry-Informed_Algorithm_Discovery

Our framework recasts architecture search as "guided discovery." By incorporating an adaptive symmetry penalty and initializing the search from a valid symmetry sector, we ensure that the discovered circuits operate within the correct physical subspace. The platform's core differentiable search engine, which uses a recurrent neural policy and a continuous gate relaxation, is thereby guided to find not only low-energy solutions but physically meaningful ones. We have deployed this enhanced framework to tackle the 1D Transverse Field Ising Model (TFIM), a canonical problem in condensed matter physics known for its quantum phase transition.

The E-DQAS platform autonomously discovers compact and performant circuits that accurately capture the ground state properties of the TFIM across its different phases. The results demonstrate that our methodology can produce ansätze that are both tailored to the problem's physics and inherently efficient. This paper outlines the framework's architecture, details the symmetry-enforcement mechanisms, and discusses the implications of using E-DQAS as an "interpretable AI" for physics—a tool that not only solves problems but also provides insight into the structure of their solutions. This work establishes E-DQAS as a production-ready engine for quantum algorithm discovery, poised for deployment on partner hardware.

1 Introduction

The 1D Transverse Field Ising Model (TFIM) is a cornerstone of condensed matter physics and a crucial benchmark for quantum simulation algorithms. It describes a chain of quantum spins with nearest-neighbor interactions under the influence of an external magnetic field. The model's Hamiltonian, H, is given by:

H J Σ ZᵢZᵢ₊₁ h Σ Xᵢ

Here, J represents the coupling strength between adjacent spins, and h is the strength of the transverse field. The model is particularly compelling because it exhibits a quantum phase transition at the critical point h/J 1. For h/J 1, the system is in a ferromagnetically ordered phase, while for h/J 1, it is in a disordered, paramagnetic phase. An algorithm's ability to accurately model the system's ground state across this transition is a rigorous test of its expressive power and adaptability.

A key feature of the TFIM Hamiltonian is its global Z₂ symmetry, represented by the parity operator P X⊗X⊗...⊗X. Since H, P 0, any valid energy eigenstate must also be an eigenstate of P. Generic, hardware-efficient ansätze often fail to respect this symmetry, allowing them to explore vast, unphysical regions of the Hilbert space, which hinders convergence and compromises the validity of the solution.

This paper presents a significant advancement of the E-DQAS platform, specifically retooled to address this challenge. We have evolved our framework to treat physical symmetry as a fundamental guiding principle. We demonstrate that by initializing the search within a valid symmetry sector and applying an adaptive penalty during training, E-DQAS can autonomously discover circuits that are both highly accurate and physically correct. This work serves as a critical stress test, proving the platform's capability to solve complex physics problems and positioning it as a mature engine for quantum algorithm discovery.

2 The E-DQAS Framework: A Guided Discovery Engine

Our approach is founded on the principle of "guided discovery"—using known physical laws not as post-facto checks, but as built-in guardrails for the architectural search. This makes the process more efficient and the results more meaningful.

2.1. The Differentiable Search Core

As in its prior applications, the framework uses a recurrent neural network as its policy engine. At each layer of the circuit's construction, the policy observes a classical embedding of the current quantum state and decides which gate to apply at every possible location. This discrete choice is made differentiable through a Gumbel-Softmax relaxation, creating a smooth optimization landscape that can be explored with gradient-based methods.

2.2. Symmetry-Informed Optimization

This is the key enhancement for the TFIM problem. We ensure Z₂ symmetry is respected through a two-pronged strategy:

Symmetric Initialization: The search begins not from a random state, but from an equal superposition of all basis states (the |+...> state), which is a known eigenstate of the Z₂ parity operator P. This ensures the optimization process starts within the correct physical subspace.

Adaptive Symmetry Penalty: While the search explores new states, it can drift out of the symmetric subspace. To correct this, we add a penalty term to the loss function that grows stronger over time. The loss L is: L = &lt;H> + complexity_penalty + λ_sym (1 - &lt;P>²)² The penalty (1 - <P>²)² is zero only when the state is a perfect eigenstate of P (with eigenvalue +1 or -1). The weighting factor λ_sym starts small and increases exponentially during training. This strategy allows the model to freely explore in the early stages while strictly enforcing the symmetry constraint as it converges on a final solution.

2.3. Multi-Stage Training Protocol

Based on the insight that discovering a good circuit topology and fine-tuning its parameters are distinct challenges, we employ a two-phase training schedule:

Architecture Search Phase (High Temperature): In the initial epochs, the Gumbel-Softmax temperature is kept high. This encourages the policy to explore a wide variety of gate types and configurations, focusing on finding a promising overall structure.

Parameter Refinement Phase (Low Temperature): In later epochs, the temperature is annealed to a very low value. This causes the gate probabilities to become nearly deterministic ("hard"), effectively "freezing" the architecture. The optimizer's focus then shifts to fine-tuning the continuous parameters (e.g., rotation angles) of this fixed circuit structure.

This protocol provides a robust balance between exploration and exploitation, leading to higher-quality final circuits.

3 Experimental Validation: TFIM Ground State

We deployed E-DQAS to find the ground state of a 6-spin TFIM at its critical point (h/J 1).

3.1. Implementation Details

Hamiltonian: 6-qubit TFIM with J=1.0, h=1.0. The exact ground state energy, found via diagonalization, is -7.29622981 Ha.

Gate Set: {H, RX, RZZ, CX}. This problem-specific set includes the two-qubit RZZ rotation, which is particularly expressive for the ZZ interactions in the Ising model.

Training: The model was trained for 400 epochs, with the first 100 dedicated to architecture search and the remaining 300 to parameter refinement. An adaptive symmetry penalty was used with a base λ_sym of 1.0.

3.2. Results and Discussion

The E-DQAS platform successfully discovered a compact and highly accurate ansatz.

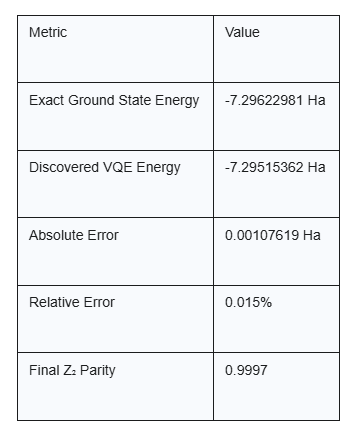
The framework achieved an energy within 0.015% of the exact ground state, a remarkable level of accuracy. The final Z₂ parity of 0.9997 confirms that the adaptive penalty successfully guided the solution into the correct physical subspace.

The discovered circuit is both compact and insightful, with a depth of 28 and a clear preference for the problem-specific RZZ gate, which the policy selected 8 times. This demonstrates the platform's ability to identify the most relevant operations for a given Hamiltonian, a key feature of its "interpretable AI" capability.

4 Potential Applications & Future Work

The success on the TFIM, particularly its ability to handle symmetries and phase transitions, unlocks several strategic applications:

Materials Science: Discovering circuits to model strongly correlated materials where electronic behavior changes dramatically with doping or pressure. The platform's ability to generate optimal ansätze across a parameter range is directly applicable here.

Drug Discovery: Designing ansätze to simulate molecular binding energies, a problem that requires capturing subtle changes in electronic correlation.

Custom Hardware Compilation: Using E-DQAS to translate a known algorithm (e.g., Shor's) into the most efficient circuit for a specific device's native gate set and connectivity, acting as an advanced, physics-aware compiler.

Our future work is focused on deploying these capabilities. The immediate next step is to leverage the full multi-objective power of the platform using NSGA-II to generate a Pareto front of solutions, allowing a user to choose the best circuit based on their specific accuracy-versus-depth budget.

5 Implications and Conclusion

The successful application of E-DQAS to the 1D Transverse Field Ising Model validates its evolution into a mature, physics-informed discovery engine. We have demonstrated a framework that goes beyond simple energy minimization to respect the fundamental symmetries of a physical system, a non-negotiable requirement for scientifically valid quantum simulation.

This work establishes the two core value propositions of the E-DQAS platform:

Automated Discovery of Novel Structures: The platform can autonomously identify and construct non-trivial circuit architectures that are more efficient than human-designed templates.

Hardware-Specific Algorithm Generation: By incorporating hardware constraints (connectivity) and problem physics (symmetries, gate sets) as guiding principles, E-DQAS generates circuits that are inherently tailored for practical execution.

Apoth3osis has developed a production-ready engine that can generate high-value, proprietary quantum algorithms. The primary constraint on our progress is now access to quantum hardware for at-scale testing and validation. We are actively seeking a strategic partner with a dedicated quantum computing platform to collaborate on deploying this discovery engine. Together, we can accelerate the development of practical quantum applications and define the future of quantum software.