APOTH3OSIS
Our tech stack is ontological
Formally verified foundations for autonomous systems
Nothing is generative
Nothing is not absence—it is formally unstable. Static void contradicts itself: enforcing singularity requires a constraint, and constraints are structure. Plurality is primitive. This forces oscillation. Balanced dynamics (0D) cross into distinction (1D) through re-entry (J = ⌐J). At the fixed points, Heyting logic crystallizes. From instability to proof—one formal chain.
"How can we get something from nothing? The answer in Laws of Form is subtle. Any given 'thing' is identical with what it is not."— Louis Kauffman
"At the lowest level, everything consists of a network of 'atoms of space' continually being updated—the entangled limit of everything computationally possible."— Stephen Wolfram
From void to verification: Built from true first principles.
Our work connects intuitionistic logic, lattice structure, and machine-checked proofs into a foundation you can ship. Proofs compile, audits are reproducible, and correctness is treated as an artifact—not a promise.
One proof, many lenses.
Like the Rosetta Stone enabled translation between scripts, our bridges transform proofs through multiple mathematical representations. Each lens preserves semantic content while revealing different structural aspects. Round-trip contracts guarantee lossless translation.
Circuit representation with crossing marks. The primordial calculus where ⌐⌐ = ⌐ and J = ⌐J.
Intuitionistic lattice of fixed points under nucleus R. The constructive core.
High-dimensional embeddings with coordinate-wise operations. Enables clustering and UMAP projection.
Pairs of elements forming oriented areas. Geometric algebra with projection to the Heyting core.
Dependency structure as directed edges. Adjacency inherits lattice order: a ≤ b implies edge.
Topological structure via Rips, Cech, or Alexandroff nerve. Betti numbers reveal holes in proof space.
structure LensModel where
R : Reentry α
Obj : Type v
[cat : Category Obj]
[monoidal : MonoidalCategory Obj]
encode : R.Omega ⥤ Obj
decode : Obj ⥤ R.Omega
round : encode ⋙ decode ≅ 𝟭 R.OmegaTransform. Preserve.
Software is mathematics.
Software is constructive mathematics. In classical logic, you can prove existence without exhibiting a witness. We don't. Every proof is a program. Every existence claim computes its object. Nucleus operators, Heyting algebras, Lean verification—structures where correctness is not asserted but constructed.
variable {α : Type u} [PrimaryAlgebra α]
structure Reentry (α : Type u) [PrimaryAlgebra α] where
nucleus : Nucleus α
primordial : α
counter : α
primordial_mem : nucleus primordial = primordial
orthogonal : primordial ⊓ counter = ⊥
... -- additional fields omitted@[simp] lemma idempotent (R : Reentry α) (a : α) :
R (R a) = R a := R.nucleus.idempotent _
@[simp] lemma le_apply (R : Reentry α) (a : α) :
a ≤ R a := Nucleus.le_apply (n := R.nucleus)
@[simp] lemma map_inf (R : Reentry α) (a b : α) :
R (a ⊓ b) = R a ⊓ R b := Nucleus.map_inf (n := R.nucleus)
@[simp] lemma map_bot (R : Reentry α) :
R (⊥ : α) = (⊥ : α) := by ... -- crossingThe nucleus operator R closes any lattice into a Heyting algebra of fixed points. In constructive mathematics, these aren't abstract objects—they're witnesses. What survives the operator computes itself. Proofs you can run. Structures that execute.
Discover. Build.
Hardware is physics.
Physics tells you what can't happen. So does ontology. Three conservation laws survive every nucleus transformation:
occamExcess(a, R(z)) = occamExcess(a, z)
Closure preserves measure. The excess above threshold survives every transformation.
theorem occam_idempotent (R : Reentry α) (a : α) :
R (occam R a) = occam R a
-- Minimal birthday fixed pointR(v) = v ↔ a ≤ v
Fixed points are exactly those above threshold. No arbitrary facts—only sufficient ones.
theorem Sufficient_iff (R : Reentry α) (a : α) :
Sufficient R a ↔ R a = a
-- Fixed point = self-sufficientsynth(T, A) = R(T ⊔ A) is least fixed ≥ T,A
Thesis meets antithesis. Closure yields the minimal stable reconciliation.
def synth (R : Reentry α) (T A : α) := R (T ⊔ A)
theorem synthesis_least (hT : T ≤ W) (hA : A ≤ W)
(hW : R W = W) : synth R T A ≤ WThese are the conservation laws of reasoning itself.
Learn. Teach.
Systems that build their own builders.
When mark and unmark become a loop, you get something that builds its own builder. Systems that operate on themselves. Closure that generates.
This principle deployed: autonomous agents with programmable budgets, guard-railed execution, and payment rails for agent commerce. Crypto infrastructure meets AI autonomy—self-modifying code with verifiable constraints.
The formal machinery of MARK. The invariant principles of UNMARK. Combined into living systems that conceive their own evolution.
→ agentpmt.comConceive. Evolve.
Research
Each project is a complete Lean 4 formalization with machine-checked proofs. The theorems compile, the invariants hold, and the code executes exactly as specified. No hand-waving—every claim is witnessed by a type-checked term.
Semantic Closure in Lean 4
Machine-verified formalization of semantic closure theory. Mechanizes how self-reference and meaning emergence arise through fixed points.
Causal Confluence in Wolfram Physics
Lean 4 proof that confluence and causal invariance are independent. Mechanizes Piskunov counterexamples with fresh-vertex semantics.
SKY Combinator Multiway Semantics
Machine-checked multiway semantics for SKY combinators with topos-theoretic gluing. Formalizes sieves as complete Heyting algebras.
Nucleus Bottleneck Autoencoder
Proof-carrying Koopman autoencoder with nucleus-constrained latent space and Lean-certified ReLU/threshold nuclei.
These are not decorative renders. Each visualization is a proof-of-concept demonstrating how Lean 4 theorems compile to executable code for computational modeling. The animations are parameterized by machine-checked invariants—what you see is the proof running.
Semantic Closure Genesis
Auto-playing cinematic of (M,R)-systems. Visuals powered by CAB-certified nuclei.
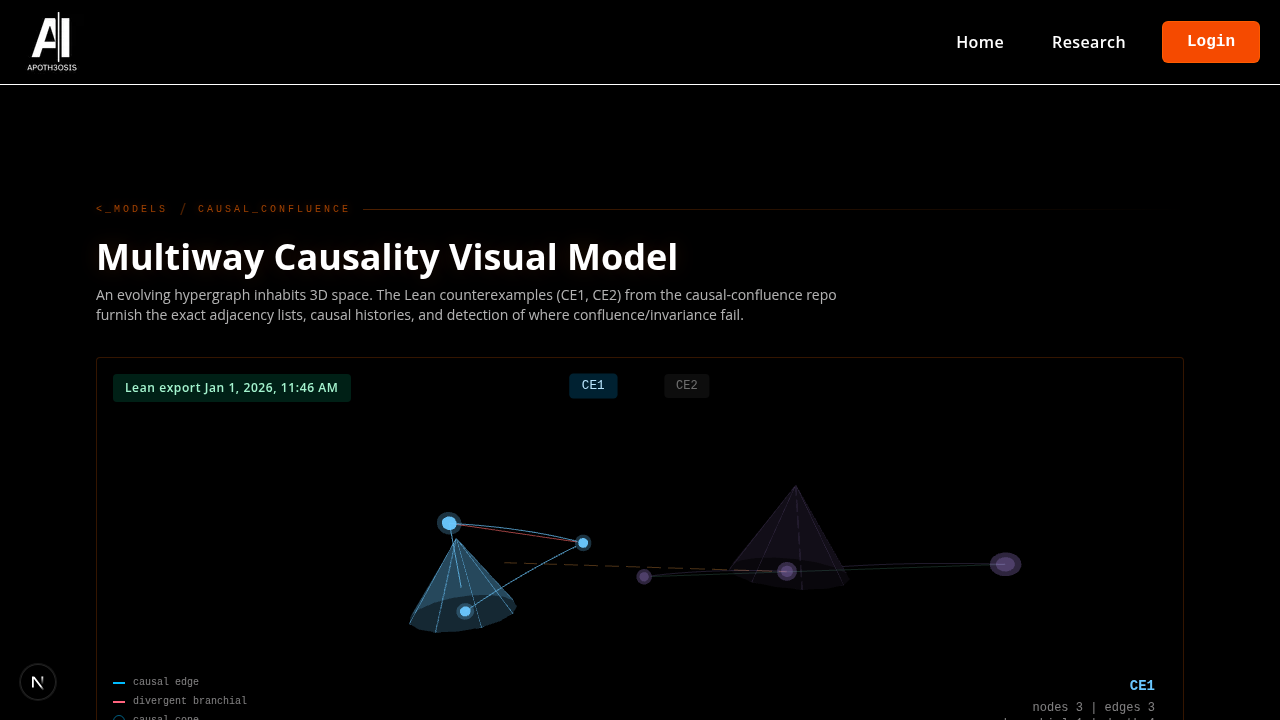
Multiway Causality
Lean counterexamples: multiway branches, causal overlays in 3D space.
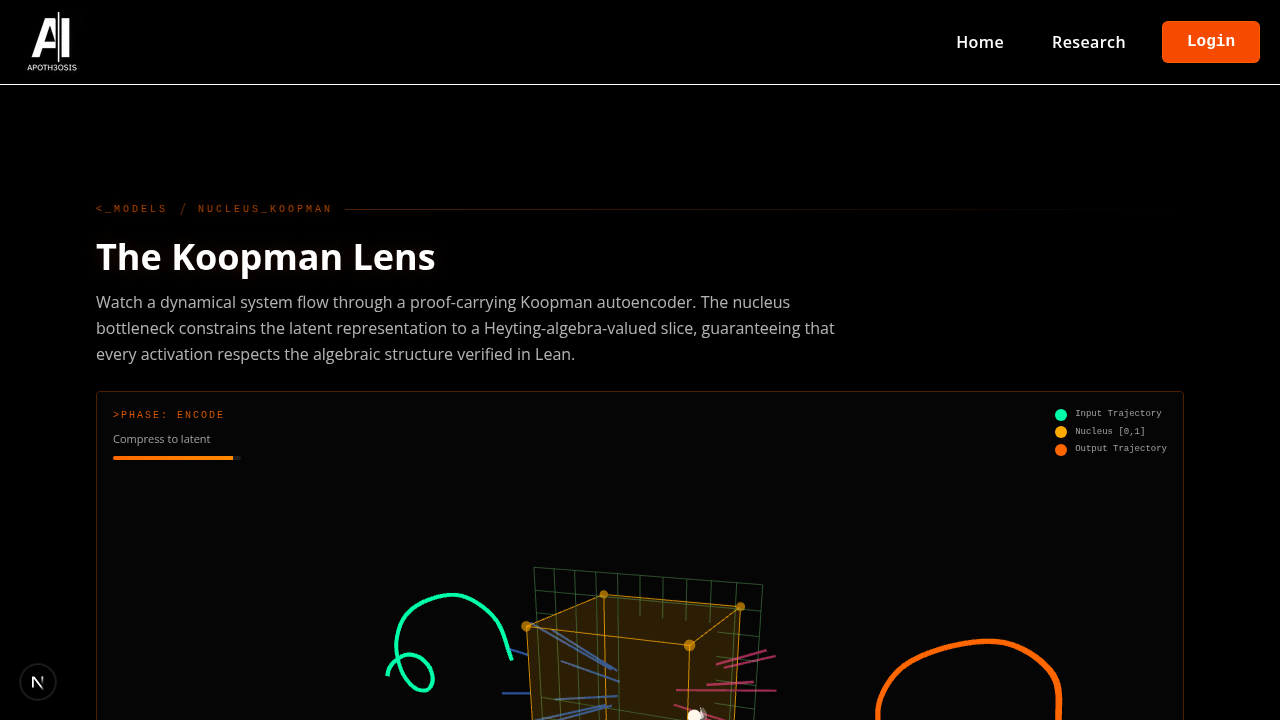
The Koopman Lens
Nucleus-constrained autoencoder. Heyting algebra preserved.
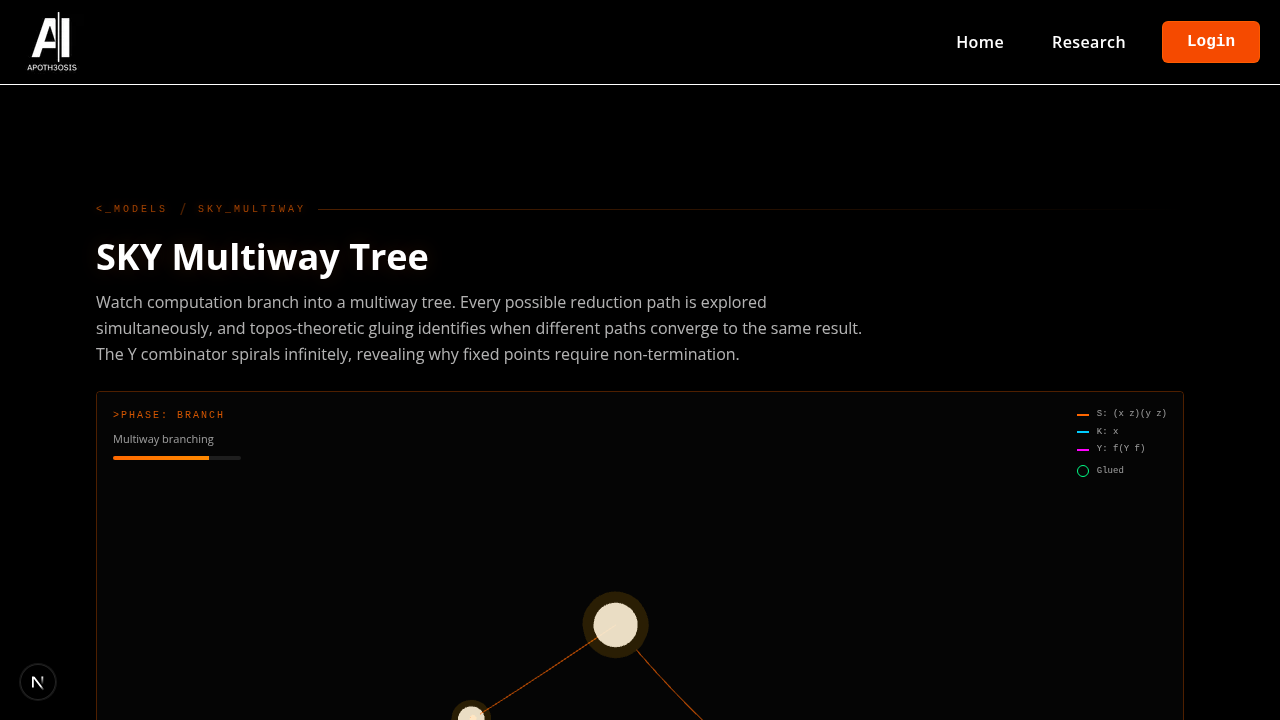
SKY Multiway Tree
Branching computation with topos-theoretic gluing.
HeytingLean: A Constructive Foundation for Verified Agent-to-Agent Computation
A machine-checked framework in Lean 4 establishing Heyting algebra as the logical substrate for provably correct agent interactions. Provides constructive proofs that guarantee computational contracts between autonomous systems.
Re-entry as a Nucleus: A Lean-Verified Heyting Core with Law-Preserving Transports
Formalizes Spencer-Brown's re-entry operator as a nucleus on lattices, yielding a Heyting algebra of fixed points verified in Lean 4. Demonstrates how self-referential closure generates intuitionistic logic from first principles.
Verified Compilation from Lean to C: A Proof-Carrying Pipeline with Minimal Trust
A complete proof-carrying pipeline that compiles Lean specifications to executable C while preserving semantic correctness at each stage. Minimizes the trusted computing base through machine-checked verification of intermediate representations.
Generative Foundations for Multiway Evolution: Unifying Laws of Form with the Wolfram Physics Project
Bridges Spencer-Brown's Laws of Form with Wolfram's multiway evolution model through Lean-verified nucleus operators. Shows how causal invariance emerges from the algebraic structure of re-entry dynamics.